前几天在群里看到有人聊到z3,正好在寒假的时候仔细研究过这个模块,今天就和大家分享下z3的简易使用方法和在ctf中该模块对于求解逆向题的帮助
简介
z3
z3是由微软公司开发的一个优秀的SMT求解器,它能够检查逻辑表达式的可满足性,通俗的来讲我们可以简单理解为它是一个解方程的计算器
SMT
SMT即可满足性模理论,它是对一个实际问题求解的特征描述,这些特征就是我们所求解的特征,SMT会使用一个或多个这样的特征描述式求解,再取每一个特征描述式所对应解的交集。
详细关于SMT的理论可以参考:https://www.cnblogs.com/steven-yang/p/7104068.html
基本数据类型
在Python中使用Z3模块,我们的所求结果一般有以下几种数据类型
Int #整型
Bool #布尔型
Array #数组
BitVec('a',8) #char型
其中BitVec可以是特定大小的数据类型,不一定是8,例如C语言中的int型可以用BitVec(‘a’,32)表示
基本语句
在Python中使用该模块,我们通常用到如下几个语句
Solver()
Solver()命令会创建一个通用求解器,创建后我们可以添加我们的约束条件,进行下一步的求解
add()
add()命令用来添加约束条件,通常在solver()命令之后,添加的约束条件通常是一个逻辑等式
check()
该函数通常用来判断在添加完约束条件后,来检测解的情况,有解的时候会回显sat,无解的时候会回显unsat
model()
在存在解的时候,该函数会将每个限制条件所对应的解集的交集,进而得出正解。
模块安装
linux下可用如下命令:
git clone https://github.com/Z3Prover/z3.git
cd z3
python scripts/mk_make.py
cd build
make
make install
z3的简单使用
求解流程
上文提到我们可以将z3理解为一个解方程的计算器,对于求解方程,我们通常会经历四个步骤:设未知数,列方程,解方程,得到正解
使用z3模块,在我的眼中也是同我们解方程一样需要经历四个步骤,下面我们简单来看一下
假设有方程组:
30x+15y=675
12x+5y=265
我们使用z3来解这个方程组:
1.设未知数
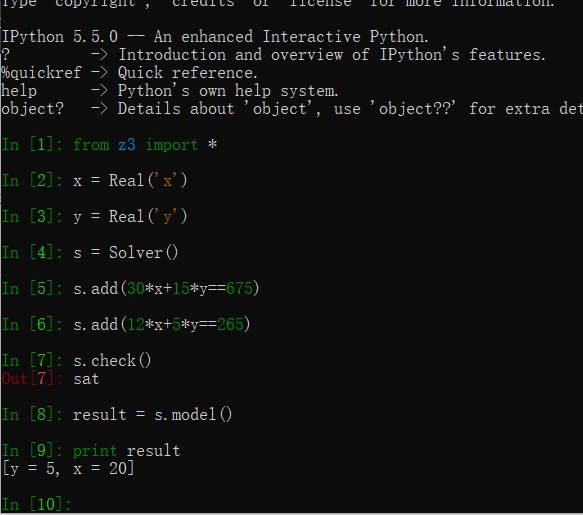
In [1]: from z3 import *
In [2]: x = Real('x')
In [3]: y = Real('y')
2.列方程
In [4]: s = Solver()
In [5]: s.add(30*x+15*y==675)
In [6]: s.add(12*x+5*y==265)
3.判断方程解的情况并解方程
In [7]: s.check()
Out[7]: sat
In [8]: result = s.model()
4.得出正解
In [9]: print result
[y = 5, x = 20]
在交互环境中,我们的求解过程如图
最终完整的代码如下:
from z3 import *
x = Real('x')
y = Real('y')
s = Solver()
s.add(30*x+15*y==675)
s.add(12*x+5*y==265)
if s.check() == sat:
result = s.model()
print result
else:
print 'no result'
可以看到我们很轻松的得到了方程组的解
利用z3解逻辑算数题
可能上面解方程组大家觉得这个模块给我们带来的方便并没有那么大,那么通过下面的题目我们或许会对z3有一个全新的认识
在网上翻了很多题目,最终我找到了15年的一道公务员考试题
这个问题的逻辑稍显复杂,我们现在用z3做一下,同样也需要经历上面四个步骤:设,列,解,得
设:2014年小李年龄:a,小李弟弟年龄:b,小王年龄:c,小王哥哥年龄:d
节省篇幅,直接写出求解代码:
from z3 import *
a = Real('a')
b = Real('b')
c = Real('c')
d = Real('d')
s = Solver()
s.add(b+2==a)
s.add(c+2==d)
s.add(a+5==d)
s.add(b+c-20-20==15)
if s.check()==sat:
print s.model()
else:
print "no result"
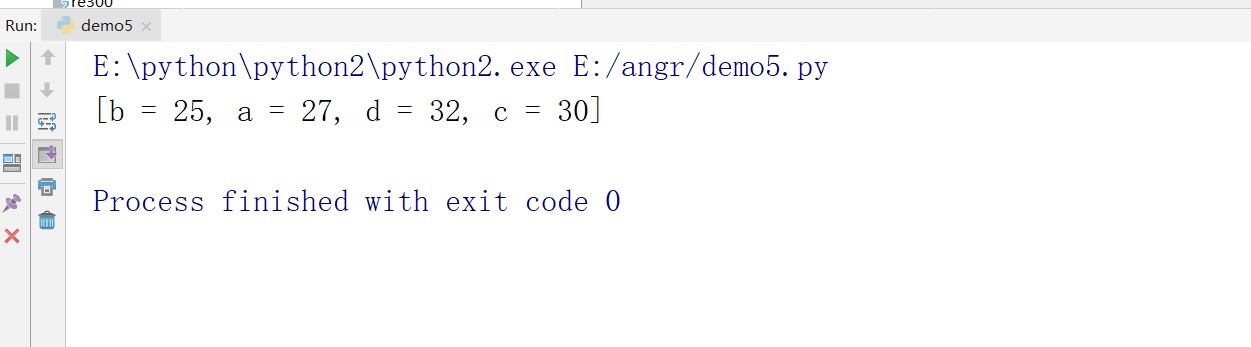
运行结果:
可以看到我们仅用几行代码就得出了答案,如果用普通的解法,我们要算4个方程所组成的方程组,所以使用z3有时候会大大增加我们的计算效率,简化我们的计算步骤。
z3在逆向题目中的应用
本篇以ISCC2018的一道RE题目为例,题目名为:My math is bad
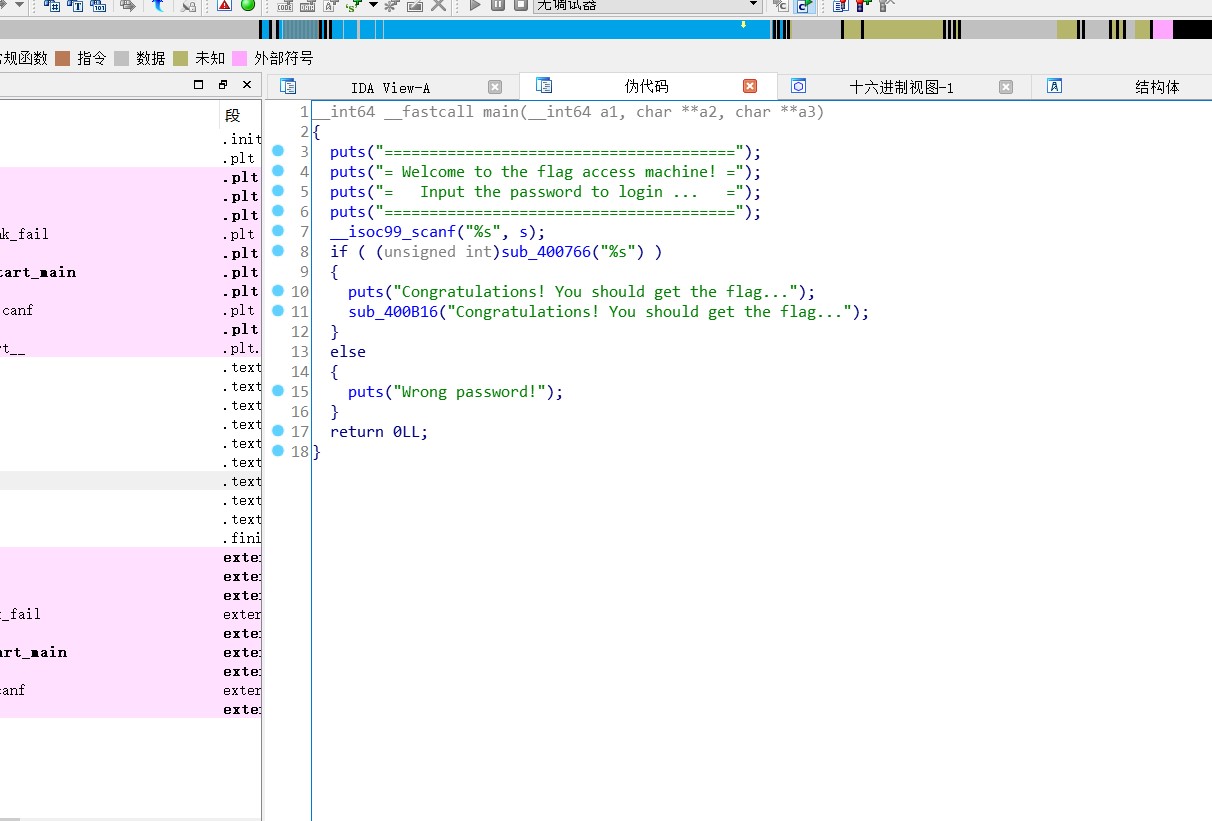
将文件拖入ida中定位到main函数,F5反编译
可以看到有一个if判断,猜测if中的函数为关键函数,进入该函数
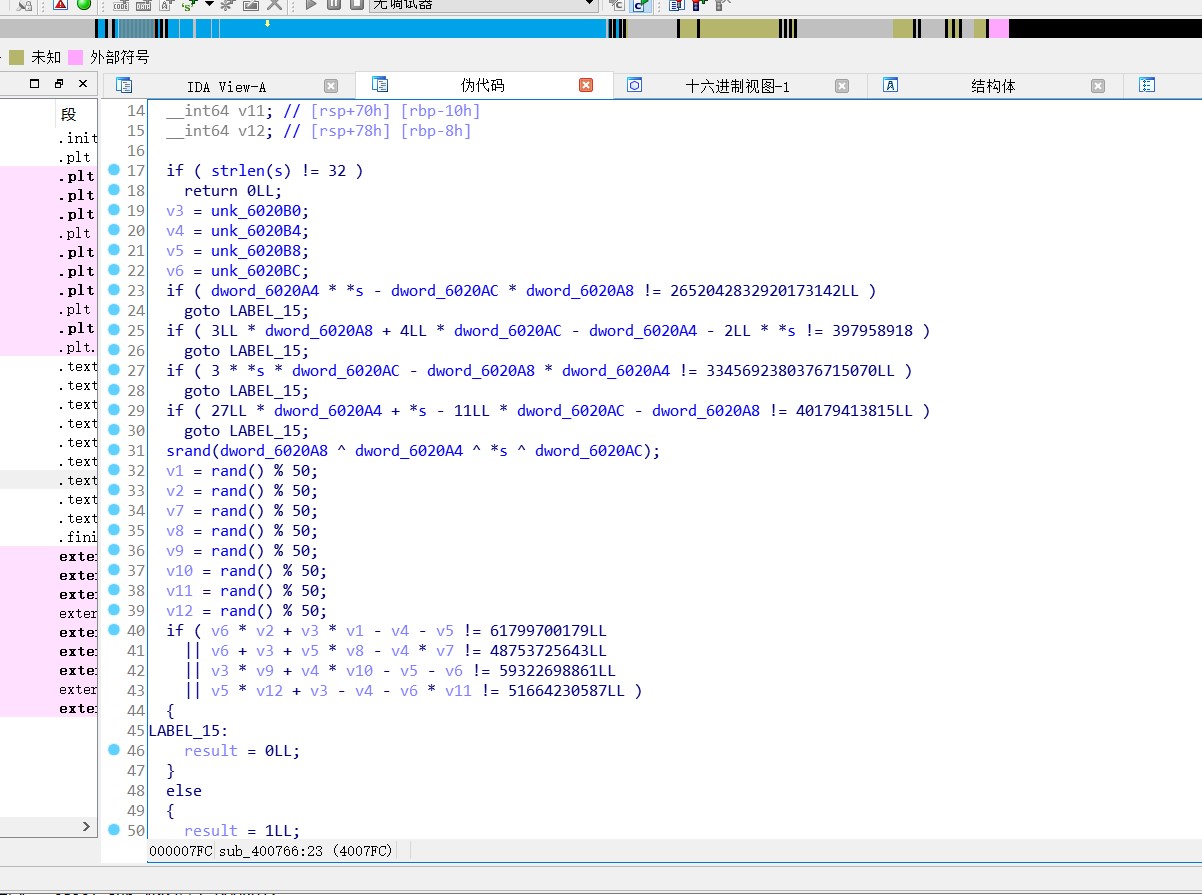
在这里看到了rand()函数,这是一个生成伪随机数的函数,所以我们几乎不可能通过逆向的方式,来将flag计算出来,继续阅读代码,发现该随机数种子是固定的,我们可以将种子计算出来,这样就可以进而获得系统生成的随机数,在计算种子的时候,我们可以使用z3模块
为了增加可读性,将关键函数的反汇编代码修饰一下:
__int64 v1; // ST40_8
__int64 v2; // ST48_8
__int64 v3; // [rsp+20h] [rbp-60h]
__int64 v4; // [rsp+28h] [rbp-58h]
__int64 v5; // [rsp+30h] [rbp-50h]
__int64 v6; // [rsp+38h] [rbp-48h]
__int64 v7; // [rsp+50h] [rbp-30h]
__int64 v8; // [rsp+58h] [rbp-28h]
__int64 v9; // [rsp+60h] [rbp-20h]
__int64 v10; // [rsp+68h] [rbp-18h]
__int64 v11; // [rsp+70h] [rbp-10h]
__int64 v12; // [rsp+78h] [rbp-8h]
if ( strlen(s) != 32 )
return 0LL;
v3 = unk_6020B0;
v4 = unk_6020B4;
v5 = unk_6020B8;
v6 = unk_6020BC;
if ( a * *s - b * c != 2652042832920173142LL )
goto LABEL_15;
if ( 3LL * c + 4LL * b - a - 2LL * *s != 397958918 )
goto LABEL_15;
if ( 3 * *s * b - c * a != 3345692380376715070LL )
goto LABEL_15;
if ( 27LL * a + *s - 11LL * b - c != 40179413815LL )
goto LABEL_15;
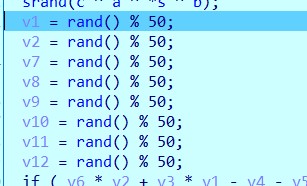
srand(c ^ a ^ *s ^ b);
v1 = rand() % 50;
v2 = rand() % 50;
v7 = rand() % 50;
v8 = rand() % 50;
v9 = rand() % 50;
v10 = rand() % 50;
v11 = rand() % 50;
v12 = rand() % 50;
if ( v6 * v2 + v3 * v1 - v4 - v5 != 61799700179LL
|| v6 + v3 + v5 * v8 - v4 * v7 != 48753725643LL
|| v3 * v9 + v4 * v10 - v5 - v6 != 59322698861LL
|| v5 * v12 + v3 - v4 - v6 * v11 != 51664230587LL )
{
LABEL_15:
result = 0LL;
}
else
{
result = 1LL;
}
return result;
}
首先我们来计算下a,s,b,c的值:
from z3 import *
a = Int('a')
b = Int('b')
s = Int('s')
c = Int('c')
l = Solver()
l.add(a*s-b*c==2652042832920173142)
l.add(3*c+4*b-a-2*s==397958918)
l.add(3 *s * b - c * a == 3345692380376715070)
l.add(27 * a + s - 11 * b - c == 40179413815)
if l.check()==sat:
print l.model()
else:
print 'no result'
然后我们计算出srand(c ^ a ^ *s ^ b);中c^a^s^b的值
c = 829124174
b = 862734414
s = 1869639009
a = 1801073242
result = a^b^c^s
print result
result的值为103643451
接下来我们继续跟进程序流程,计算rand函数所生成的几个值
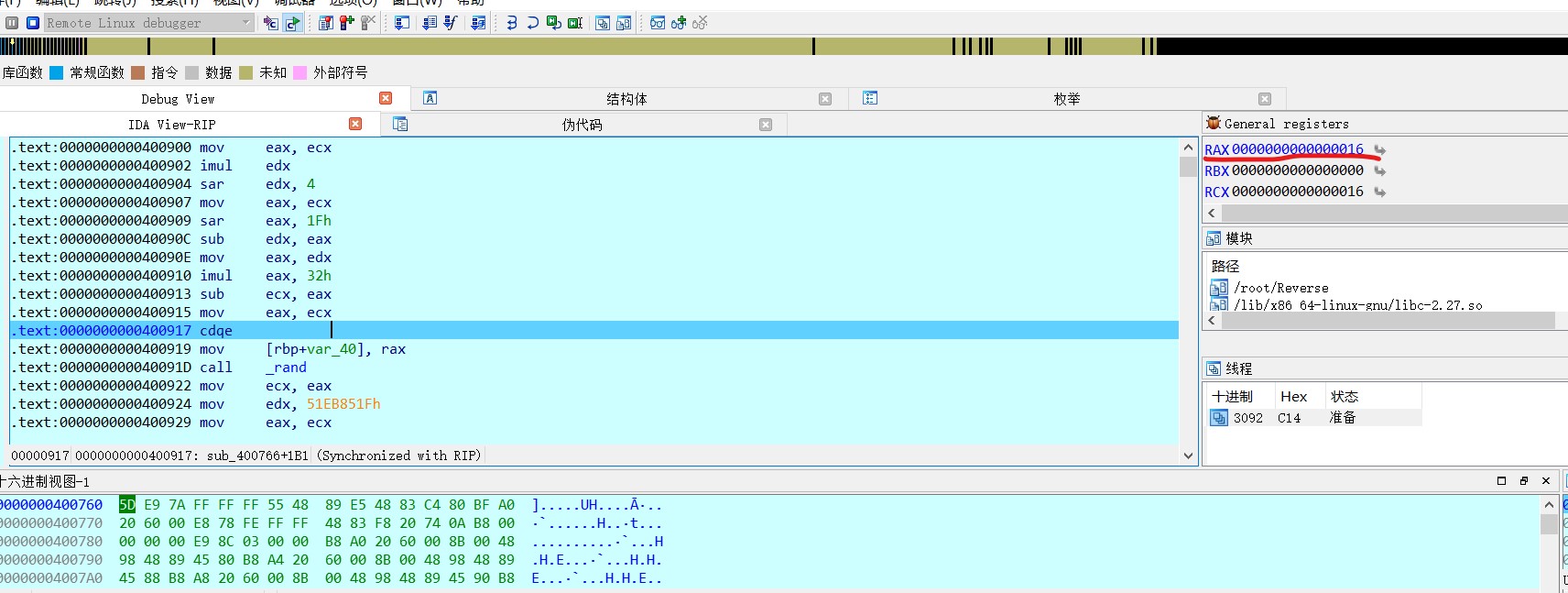
使用ida动态调试程序,跳转到srand()函数,因为是直接跳过来的,srand()还没有参数,而刚才我们已将该参数的值通过z3计算了出来,所以在程序运行到mov edi, eax时,直接将eax的值改为103643451即可
然后我们跟进程序,得到了v1的值
继续跟进获得了下面的几个生成值
v1 = 0x16
v2 = 0x27
v7 = 0x2d
v8= 0x2d
v9 = 0x23
v10= 0x29
v11 = 0xd
v12 = 0x24
接着我们到了if的判断
其中v3 v4 v5 v6是未知的,所以在这里我们可以设四个未知数,其他数我们通过前面已经计算出来了,使用z3求解这四个未知数即可
from z3 import *
v3 = Int('v3')
v4 = Int('v4')
v5 = Int('v5')
v6 = Int('v6')
v1 = 0x16
v2 = 0x27
v7 = 0x2d
v8= 0x2d
v9 = 0x23
v10= 0x29
v11 = 0xd
v12 = 0x24
l = Solver()
l.add(v6 * v2 + v3 * v1 - v4 - v5 == 61799700179)
l.add(v6 + v3 + v5 * v8 - v4 * v7 == 48753725643)
l.add(v3 * v9 + v4 * v10 - v5 - v6 == 59322698861)
l.add(v5 * v12 + v3 - v4 - v6 * v11 == 51664230587)
if l.check() == sat:
print l.model()
else:
print 'no result'
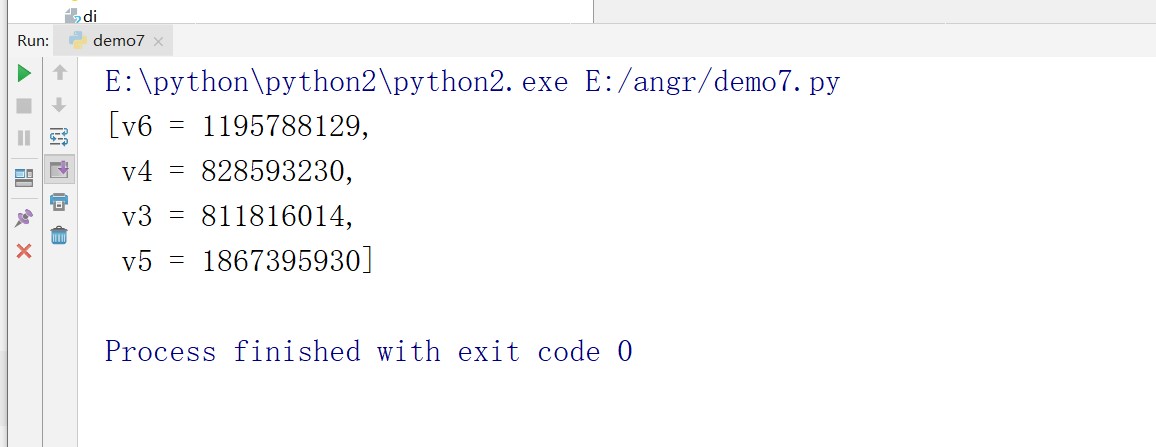
运行结果
至此我们需要输入的值都计算出来了
c = 829124174
b = 862734414
s = 1869639009
a = 1801073242
v6 = 1195788129
v4 = 828593230
v3 = 811816014
v5 = 1867395930
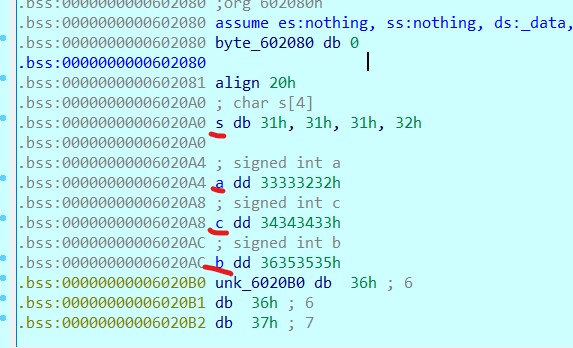
这里我们需要将abcs的顺序确定一下,在bss段中可看到其顺序
然后我们需要将这些数字转换为字符串输入,这里用到了libnum库
import libnum
c = 829124174
b = 862734414
s = 1869639009
a = 1801073242
v6 = 1195788129
v4 = 828593230
v3 = 811816014
v5 = 1867395930
array = [s,a,c,b,v3,v4,v5,v6]
result = ""
for i in array:
result = result + libnum.n2s(i)[::-1]
print result
运行脚本
将字符串输入后我们即可得到flag
总结
z3是一个强大的约束求解器,它不仅能处理一些看起来很复杂的逻辑问题,在逆向领域中往往可以简化我们计算步骤,增加求解效率,尤其是在ctf比赛中一些繁杂的RE题目通过z3来解往往显得非常简单,我们在解决问题时如果能灵活应用z3,往往会有意想不到的效果。